您所在的位置：首页 - 科技 - 正文科技

小角度耦合双摆的拉格朗日力学分析

奚诗科技 05-31 【科技】 881人已围观

摘要在物理学中，耦合双摆是一个经典的动力学问题，涉及到两个摆的运动如何相互影响。通过拉格朗日力学可以比较方便地描述这种系统的运动规律。本文将根据《张朝阳的物理课》中的推导，对小角度耦合双摆进行拉格朗日力学

在物理学中，耦合双摆是一个经典的动力学问题，涉及到两个摆的运动如何相互影响。通过拉格朗日力学可以比较方便地描述这种系统的运动规律。本文将根据《张朝阳的物理课》中的推导，对小角度耦合双摆进行拉格朗日力学分析。

1. 双摆系统的建模

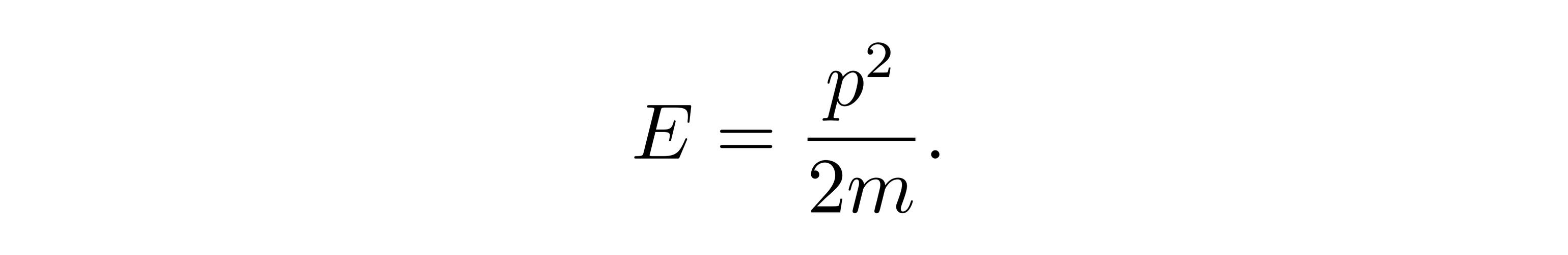
考虑两个长度为 l1 和 l2 的摆，分别以 θ1 和 θ2 表示它们相对竖直方向的偏角。双摆系统的势能可以表示为：

\[ V = m_1 g l_1 \cos(\theta_1) m_2 g (l_1 \cos(\theta_1) l_2 \cos(\theta_2)) \]

其动能可以表示为：

\[ T = \frac{1}{2} m_1 (\dot{l_1}^2 l_1^2 \dot{\theta_1}^2) \frac{1}{2} m_2 ((\dot{l_1}^2 l_1^2 \dot{\theta_1}^2) (\dot{l_2}^2 l_2^2 \dot{\theta_2}^2) 2 l_1 l_2 \dot{\theta_1} \dot{\theta_2} \cos(\theta_1 \theta_2)) \]

2. 拉格朗日方程的推导

根据拉格朗日力学，系统的 Lagrange 函数可以表示为：

\[ L = T V \]

通过对 θ1 和 θ2 的 EulerLagrange 方程求解，可以得到系统的运动方程。在小角度近似下，我们可以忽略高次项，得到简化后的运动方程：

\[ (m_1 m_2) l_1 \ddot{\theta_1} m_2 l_2 \ddot{\theta_2} \cos(\theta_1 \theta_2) m_2 l_2 \dot{\theta_2}^2 \sin(\theta_1 \theta_2) = (m_1 m_2) g \theta_1 \]

\[ m_2 l_2 \ddot{\theta_2} m_2 l_1 \ddot{\theta_1} \cos(\theta_1 \theta_2) m_2 l_1 \dot{\theta_1}^2 \sin(\theta_1 \theta_2) = m_2 g \theta_2 \]

这就是双摆系统在小角度近似下的运动规律，描述了两个摆的运动如何相互影响。